How To Draw A Hyperbola
How To Draw A Hyperbola - The lines through the corners of this rectangle are the asymptotes. If the coefficient of \(x^{2}\) is positive, draw the branches of the hyperbola opening left and right through the points determined by \(a\). This is the axis on which the two foci are. Web sketch and extend the diagonals of the central rectangle to show the asymptotes. Web to graph a hyperbola, follow these simple steps: Each of the fixed points is called a focus of the hyperbola. Label the foci and asymptotes, and draw a smooth curve to form the hyperbola, as shown in figure 8. Length of major axis = 2a, and length of minor axis = 2b. Use the hyperbola formulas to find the length of the major axis and minor axis. A hyperbola is the set of all points (x, y) (x, y) in a plane such that the difference of the distances between (x, y) (x, y) and the foci is a positive constant. Sticking with the example hyperbola. A 2 + b 2 = c 2. Use the hyperbola formulas to find the length of the major axis and minor axis. The line through the foci, is called the transverse axis. To determine the foci you can use the formula: Sticking with the example hyperbola. Web learn how to graph hyperbolas. The graph approaches the asymptotes but never actually touches them. The line through the foci, is called the transverse axis. Creating a rectangle to graph a hyperbola with asymptotes. A 2 + b 2 = c 2. Creating a rectangle to graph a hyperbola with asymptotes. This is the axis on which the two foci are. Web the equations of the asymptotes are y = ±a b(x−h)+k y = ± a b ( x − h) + k. Web these points are what controls the entire shape of the. Label the foci and asymptotes, and draw a smooth curve to form the hyperbola, as shown in figure 8. The graph approaches the asymptotes but never actually touches them. To graph a hyperbola from the equation, we first express the equation in the standard form, that is in the form: The central rectangle and asymptotes provide the framework needed to. If the coefficient of \(x^{2}\) is positive, draw the branches of the hyperbola opening left and right through the points determined by \(a\). Web use these points to draw the fundamental rectangle; The two points where the transverse axis intersects the hyperbola are each a vertex of. Web to graph a hyperbola, follow these simple steps: This is the axis. Remember to switch the signs of the numbers inside the parentheses, and also remember that h is inside the parentheses with x, and v is inside the parentheses with y. Web to graph a hyperbola, follow these simple steps: Label the foci and asymptotes, and draw a smooth curve to form the hyperbola, as shown in figure 8. A 2. Notice that the definition of a hyperbola is very similar to that of an ellipse. Web learn how to graph hyperbolas. The two points where the transverse axis intersects the hyperbola are each a vertex of. This is the axis on which the two foci are. The graph approaches the asymptotes but never actually touches them. The lines through the corners of this rectangle are the asymptotes. Length of major axis = 2a, and length of minor axis = 2b. Use the hyperbola formulas to find the length of the major axis and minor axis. The two points where the transverse axis intersects the hyperbola are each a vertex of. Using the hyperbola formula for the. The graph approaches the asymptotes but never actually touches them. The two points where the transverse axis intersects the hyperbola are each a vertex of. To graph a hyperbola from the equation, we first express the equation in the standard form, that is in the form: Web sketch and extend the diagonals of the central rectangle to show the asymptotes.. Use the hyperbola formulas to find the length of the major axis and minor axis. Web these points are what controls the entire shape of the hyperbola since the hyperbola's graph is made up of all points, p, such that the distance between p and the two foci are equal. The two points where the transverse axis intersects the hyperbola. The two lines that the. Web like the ellipse, the hyperbola can also be defined as a set of points in the coordinate plane. To determine the foci you can use the formula: The central rectangle and asymptotes provide the framework needed to sketch an accurate graph of the hyperbola. Web this step gives you two lines that will be your asymptotes. Label the foci and asymptotes, and draw a smooth curve to form the hyperbola, as shown in figure 8. Web use these points to draw the fundamental rectangle; This is the axis on which the two foci are. A hyperbola is the set of all points (x, y) (x, y) in a plane such that the difference of the distances between (x, y) (x, y) and the foci is a positive constant. Web sketch and extend the diagonals of the central rectangle to show the asymptotes. Remember to switch the signs of the numbers inside the parentheses, and also remember that h is inside the parentheses with x, and v is inside the parentheses with y. Web the equations of the asymptotes are y = ±a b(x−h)+k y = ± a b ( x − h) + k. The two points where the transverse axis intersects the hyperbola are each a vertex of. The graph approaches the asymptotes but never actually touches them. Web to graph a hyperbola, follow these simple steps: Creating a rectangle to graph a hyperbola with asymptotes.
Easy Steps to Draw A Hyperbola using Focus Directrix Method Engg

HOW TO DRAW THE RECTANGULAR HYPERBOLA IN ENGINEERING DRAWING YouTube
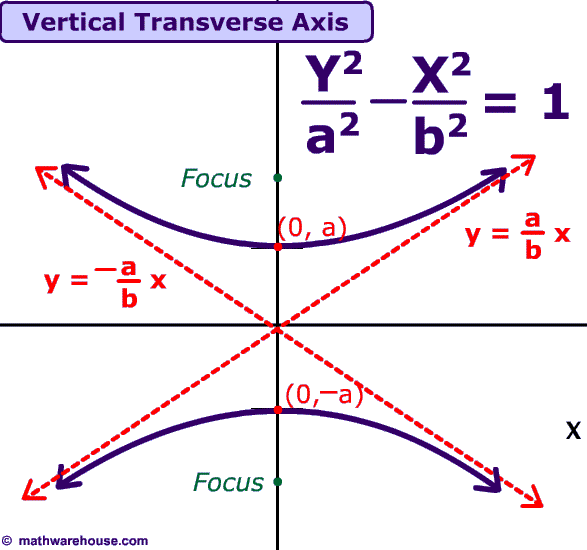
Formula and graph of a hyperbola. How to graph a hyperbola based on its

How to Draw a HYPERBOLA in Engineering Drawing What is a Hyperbola
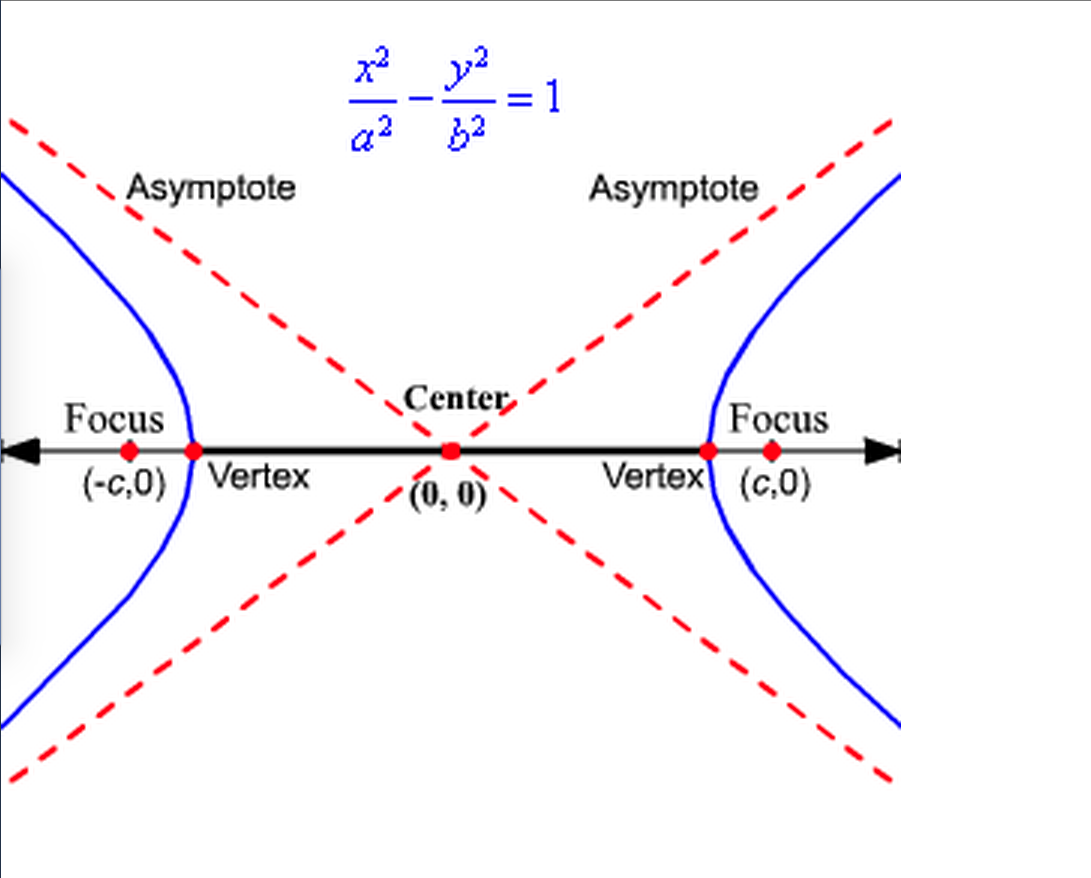
What is a hyperbola?

Easy Steps to Draw A Hyperbola using Focus Directrix Method Engg

HOW TO DRAW A HYPERBOLA USING LOCUS METHOD LOCI ENGINEERING
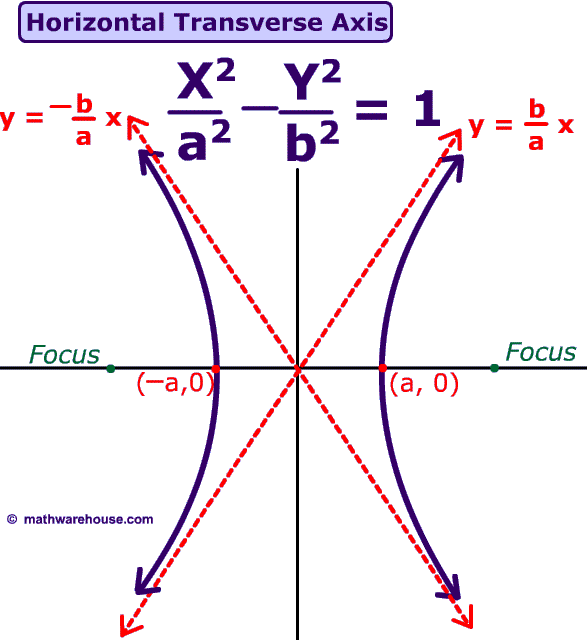
Formula and graph of a hyperbola. How to graph a hyperbola based on its
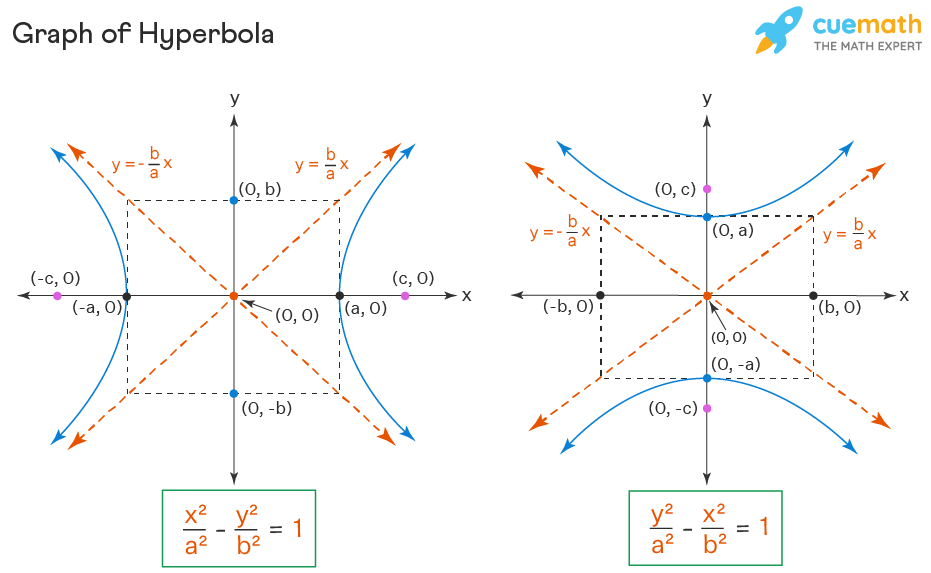
Hyperbola Equation, Properties, Examples Hyperbola Formula

How to draw a Hyperbola by Arcs of Circle Method YouTube
Length Of Major Axis = 2A, And Length Of Minor Axis = 2B.
Using The Hyperbola Formula For The Length Of The Major And Minor Axis.
A 2 + B 2 = C 2.
Web Learn How To Graph Hyperbolas.
Related Post: