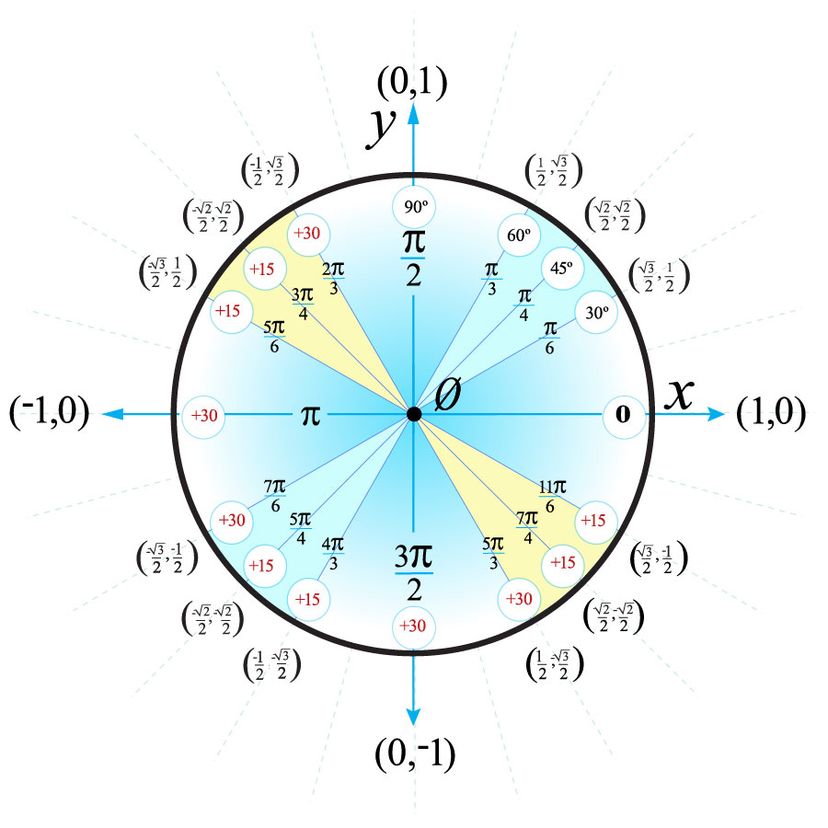
Unit Circle Drawing
Unit Circle Drawing - We can see things in their simplest form. What is the equation for the unit circle? Let's get an intuition of the unit circle by using the interactive below. Web learn the equation of a unit circle, and know how to use the unit circle to find the values of various trigonometric ratios such as sine, cosine, tangent. Web the unit circle makes things easier, not harder. Draw an equilateral triangle with side length 2. A point with coordinates (1;0) will correspond to. What is meant by “wrapping the number line around the unit circle?” how is this used to identify real numbers as the lengths of arcs on the unit circle? We have already defined the trigonometric functions in terms of right triangles. No matter how big or small the triangle is. Note that not all instructors like to see pictures. For this purpose, draw a unit circle in the xoy coordinate circle. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Web x 2 + y 2 = 1. In this section, we will redefine them in terms of the unit circle. So why is it so useful? How to memorize unit circle? Web finding trigonometric functions using the unit circle. What is a unit circle? Web what is the unit circle and why is it important in trigonometry? A point with coordinates (1;0) will correspond to. Recall that a unit circle is a circle centered at the origin with radius 1, as shown in figure 2. Don't try to rely only on your memory. Web to do so, we need to define the type of circle first, and then place that circle on a coordinate system. The angle. How do we associate an arc on the unit circle with a closed interval of real numbers? Welcome to the unit circle calculator ⭕. Using the formula s = rt, and knowing that r = 1, we see that for a unit circle, s = t. In this section, we will redefine them in terms of the unit circle. The. Split it down the middle. Don't try to rely only on your memory. Use pythagoras’ theorem to find the new side’s length. Mark the basic angles in degrees (0, 90, 180, 270) or in radians (0, π/2, π, 3π/2). Unit circle tangent & other trig functions. How to memorize unit circle? For a given angle θ each ratio stays the same. The angle (in radians) that t intercepts forms an arc of length s. Using the formula s = rt, and knowing that r = 1, we see that for a unit circle, s = t. Web the unit circle is a circle with a radius. Remember that each internal angle of an equilateral triangle is 60°, so the halved angle is 30°. In a circle or on a graph. How to memorize unit circle? We can see things in their simplest form. Web x 2 + y 2 = 1. No matter how big or small the triangle is. For this purpose, draw a unit circle in the xoy coordinate circle. A point with coordinates (1;0) will correspond to. Using the formula s = rt, and knowing that r = 1, we see that for a unit circle, s = t. Don't try to rely only on your memory. No matter how big or small the triangle is. Also check out the examples, faqs. Mark the basic angles in degrees (0, 90, 180, 270) or in radians (0, π/2, π, 3π/2). Draw an equilateral triangle with side length 2. Our tool will help you determine the coordinates of any point on the unit circle. Unit circle tangent & other trig functions. The unit circle is simple, it's a circle with a radius of 1. For a given angle θ each ratio stays the same. What is a unit circle? Web to define our trigonometric functions, we begin by drawing a unit circle, a circle centered at the origin with radius 1, as shown in. Mark the basic angles in degrees (0, 90, 180, 270) or in radians (0, π/2, π, 3π/2). This line is at right angles to the hypotenuse at the unit circle and touches the unit circle only at that point (the tangent point). The unit circle is simple, it's a circle with a radius of 1. How to memorize unit circle? When you work with angles in all four quadrants, the trig ratios for those angles are computed in terms of the values of x, y, and r, where r is the radius of the circle that corresponds to the hypotenuse of the right triangle for your angle. No matter how big or small the triangle is. We have already defined the trigonometric functions in terms of right triangles. How do we associate an arc on the unit circle with a closed interval of real numbers? Web what is the unit circle and why is it important in trigonometry? In fact, these three right triangles are going to be determined by counting the fingers on your left hand! Then, use soh cah toa on the triangle. Point (cosine of theta, sine of theta) is located near one thirty o'clock on the circle. The angle (in radians) that \(t\) intercepts forms an arc of length \(s\). Sine, cosine and tangent (often shortened to sin, cos and tan) are each a ratio of sides of a right angled triangle: This is true for all points on the unit circle, not just those in the first quadrant, and is useful for defining the trigonometric functions in terms of the unit circle. Split it down the middle.
Unit Circle Quick Lesson Downloadable PDF Chart · Matter of Math
Unit Circle Labeled With Quadrantal Angles And Values ClipArt ETC
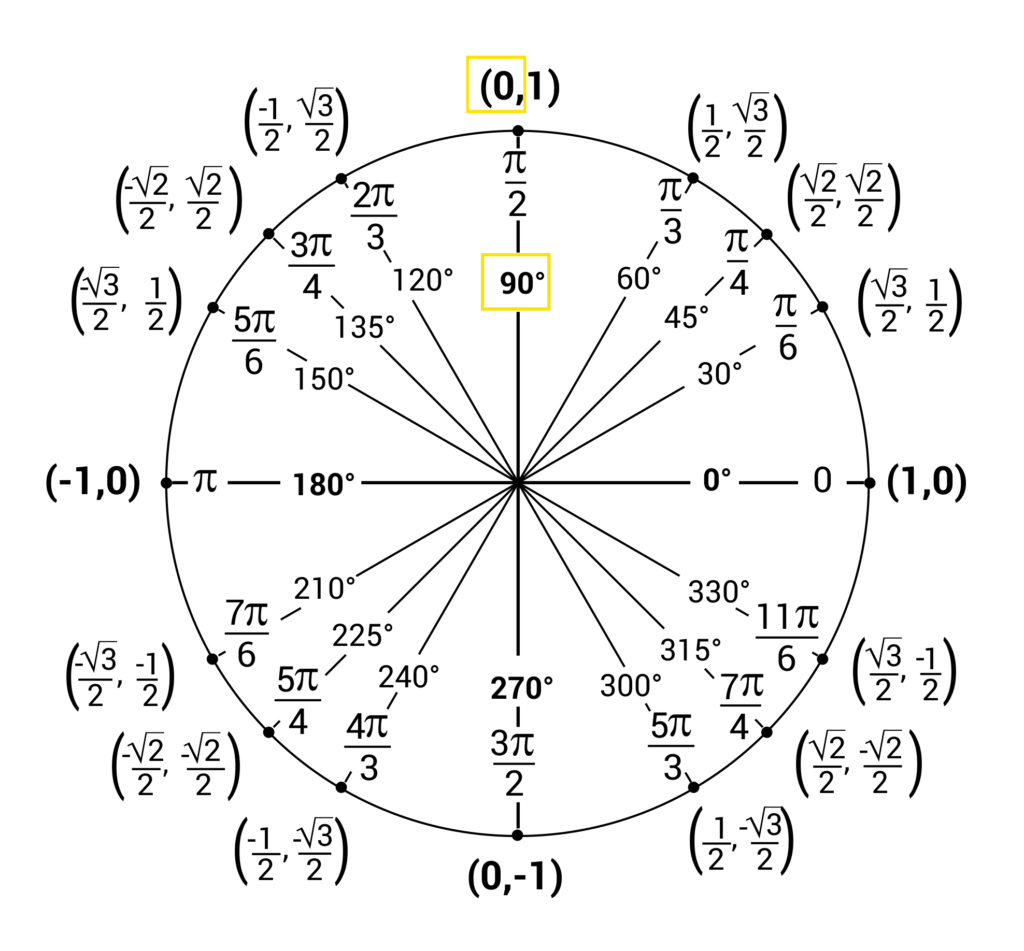
Unit Circles and Standard Position (Video & Practice Questions)
How to Use the Unit Circle in Trigonometry HowStuffWorks
Unit Circle Labeled At Special Angles ClipArt ETC

Unit circle Solved Examples Geometry Cuemath

Unit Circle Quick Lesson Printable PDF Chart · Matter of Math
Unit Circle Labeled With Special Angles And Values ClipArt ETC

Unit Circle Diagrams Classful
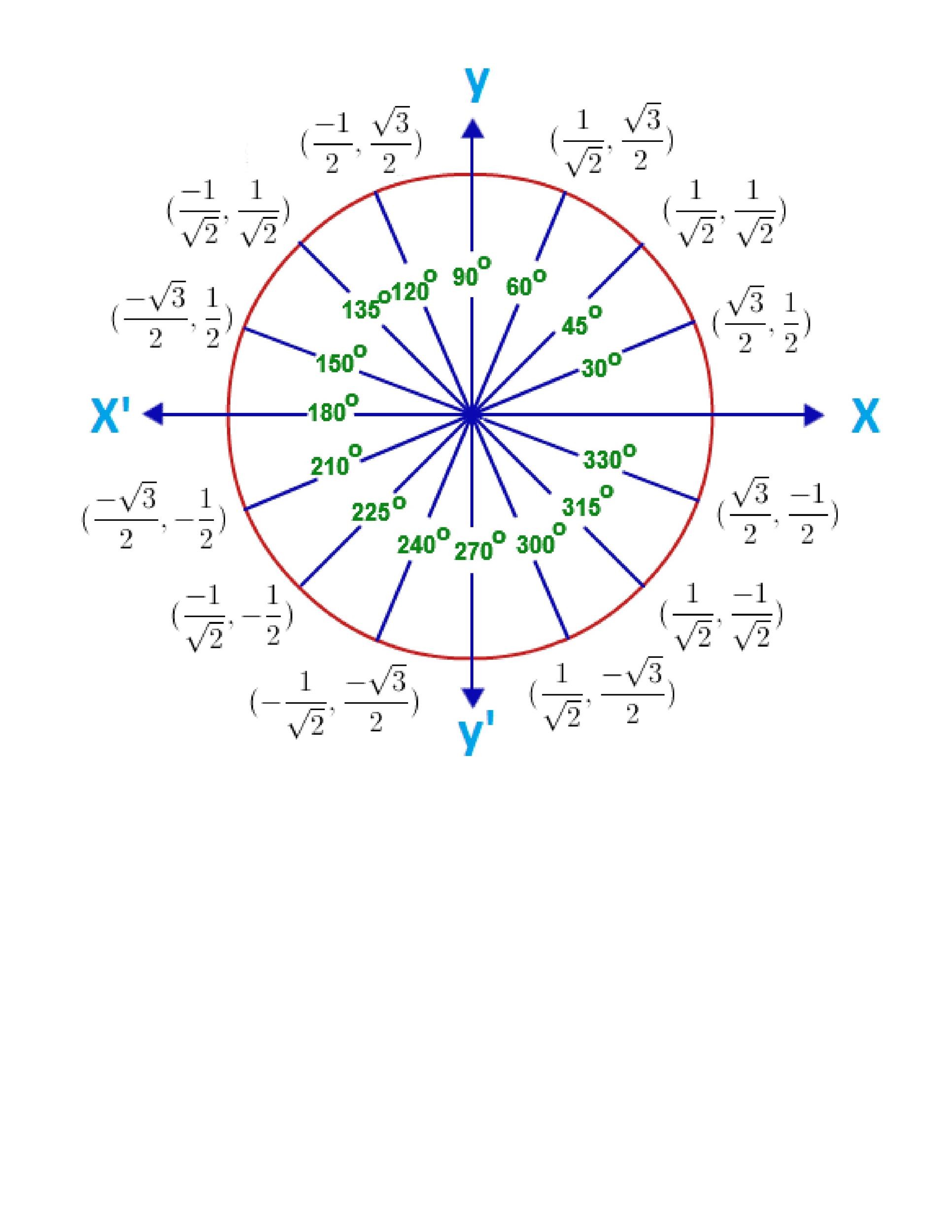
42 Printable Unit Circle Charts & Diagrams (Sin, Cos, Tan, Cot etc)
You Don't Need To Memorize The Entire.
Unit Circle Tangent & Other Trig Functions.
A Point With Coordinates (1;0) Will Correspond To.
We Can See Things In Their Simplest Form.
Related Post: